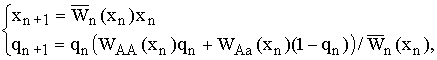
(2.1)
На правах рукописи
Работа выполнена в Институте автоматики и процессов управления ДВО РАН
| Научный руководитель – | доктор биологических наук, профессор Фрисман Ефим Яковлевич. |
| Официальные оппоненты: | доктор физико-математических наук, профессор Цициашвили Гурами Шалвович; |
|
доктор биологических наук, профессор Пудовкин Александр Иванович. | |
| Ведущая организация: |
Институт проблем морских технологии ДВО |
Защита состоится "10" ноября 2006 года в 10 часов на заседании
диссертационного совета ДМ 005.007.03 в Институте автоматики и
процессов управления ДВО РАН по адресу: 690041, г. Владивосток,
ул. Радио, 5.
С диссертацией можно ознакомиться в библиотеке Института автоматики
и процессов управления ДВО РАН.
Автореферат разослан "10" октября 2006 г.
| Ученый секретарь диссертационного совета | М.Ю. Черняховская |
Актуальность работы. Динамическая теория популяций традиционно рассматривается как смежный раздел теоретической популяционной экологии (Федоров, Гильманов, 1980) и популяционной биофизики (Базыкин, 1985; Волькенштейн, 1988; Романовский, 2004; Чернавский, 2004). Основная проблема, вокруг которой формируется динамическая теория – это описание характера и объяснение механизмов флюктуирующего (квазипериодического и хаотического) поведения численности популяций. К этой проблеме примыкает важная прикладная задача разработки оптимальной стратегии эксплуатации промысловых видов (оптимизация процесса "сбора урожая"). По смыслу рассматриваемых задач ясно, что в теоретической популяционной экологии проводятся исследования динамики лимитированных популяций, развивающихся в условиях ограниченности ресурсов жизнедеятельности.
С 30-х годов ХХ-го века бурно развивается другая ветвь динамической популяционной теории – математическая популяционная генетика, в рамках которой строятся и исследуются модели эволюционного преобразования генетической структуры популяции. Особенности динамики численности при этом обычно не анализировались. Численность считалась либо "достаточно" (фактически неограниченно) большой (в детерминированных моделях) либо неизменной (модели, используемые для анализа последствий генетического дрейфа).
Попытки объединить популяционно-экологические и популяционно-генетические подходы высветили два типа проблем, которые могут быть рассмотрены в рамках этой теории. Во-первых, здесь получило естественное развитие исследование действия эволюционных факторов, в первую очередь, естественного отбора, на изменение генетической структуры, а соответственно и изменений характера динамики популяций, развивающихся в условиях ограниченности экологических ресурсов (т.е. находящихся под действием лимитирующих факторов окружающей среды). Интересные частные результаты были получены Дж. Райгарденом (Rougharden, 1971) и Б. Чарлзуорсом (Charlesworth, 1971). Первый из этих исследователей численно проанализировал дискретную математическую модель динамики частот аллелей в менделевской однолокусной диаллельной популяции (с линейным видом зависимости приспособленности от численности) для случаев стационарной и флюктуирующей среды обитания. Б. Чарлзуорс исследовал аналитически более общую дискретную модель эволюции однолокусной менделевской популяции, развивающуюся в стационарной среде. Мощное развитие этих результатов было получено во многих работах и сформулировано в виде концепции К и r-отбора. В частности для метапопуляции с неполовым размножением оно было выполнено в работах Е.В. Евдокимова (Евдокимов, 1999).
Во-вторых, в рамках эволюционно-экологических моделей оказался возможен подробный анализ эволюционно-генетических последствий промысла. Господствующая в теории оптимальной эксплуатации концепция максимального уравновешенного изъятия предполагает поддержание численности промысловой популяции на уровне, обеспечивающем максимальное воспроизводство. Таким образом, популяции, подверженные промыслу, оказываются в других экологических условиях, чем неэксплуатируемые популяции, имеющие численность, определяемую балансами естественных процессов. В результате в промысловых популяциях могут изменяться условия отбора, а соответственно и приспособленности генотипических групп особей.
В последнее время в большой серии современных исследований отмечено почти катастрофическое снижение эффективной численности популяций и потеря генетического разнообразия в результате антропогенного воздействия. Эти негативные для биологических видов тенденции наблюдаются не только в промышляемых популяциях (например, изменение генетической структуры породообразующих деревьев при восстановлении лесов после вырубки, промысловых видов рыб), но и в популяциях, которые явно не эксплуатируются, а испытывают на себе влияние антропогенного воздействия за счет фрагментации и сокращения среды обитания (например, генетические изменения в популяции саламандры). Окончательное решение вопроса, что происходит с адаптивной изменчивостью видов на фоне антропогенного воздействия, не является очевидным и тоже привлекает интерес исследователей (например, Singh, 1978; Martínez-Garmendia, 1998).
Подробного исчерпывающего анализа описанных выше проблем до последнего времени не проводилось. Данная работа призвана заполнить некоторые пробелы в этой области.
Цель работы. Целью работы является описание и исследование наиболее простой модельной ситуации, в которой проявляются закономерности взаимосвязанных изменений динамики генетической структуры и численности популяций, вызванных взаимодействием эволюционных (в основном селективных) и экологических (ограничивающих популяционный рост) факторов, включая эффекты промыслового воздействия на эксплуатируемые популяции. В качестве такой модельной системы рассматривается диплоидная менделевская панмиктичная популяция, генетическое разнообразие в которой контролируется одним диалелльным локусом, экологическое лимитирование сводится к убывающей зависимости приспособленности от численности, а воздействие промысла – к изъятию части особей.
В ходе работы необходимо решить следующие задачи.
Достоверность и обоснованность результатов, полученных в работе, определяется использованием классических методов построения и исследования математических моделей динамики популяции экосистем на основе аппарата рекуррентных уравнений (Шапиро, Луппов, 1983), элементов качественной теории бифуркаций (Хенон, 1981; Мун, 1990), методов математического анализа.
Научная новизна заключается в следующем:
Практическая ценность работы. Проведенная работа вносит вклад в исследования последствий промыслового воздействия. Детально описаны стратегии промысла, приводящие к кардинально различающимся режимам динамики численности и генетического состава. Полученные результаты и выводы возможно использовать при решении задач оценки и сохранения биоразнообразия и рационального природопользования.
Апробация работы. Результаты диссертационной работы докладывались и обсуждались на Дальневосточной конференции "Молодежь и научно-технический прогресс" (Владивосток, 1998, 2000); на 1-ой, 3-ей, 4-ой, 5-ой и 6-ой Дальневосточных конференциях студентов и аспирантов по математическому моделированию (Владивосток, 1997, 1999, 2000, 2001, 2002); на Дальневосточной математической школе-семинаре им. академика Е.В. Золотова (Владивосток, 2000, 2001, 2002, 2003, 2004, 2005); на научной конференции "Вологдинские чтения" (Владивосток, 2000); на Всероссийских конференциях по моделированию неравновесных систем (Красноярск, МНС-2000,МНС-2001, МНС-2002, МНС-2003); на 6-ой Международной конференции "Экология и здоровье человека. Экологическое образование. Математические модели и информационные технологии" (Краснодар, 2001); на конференции, посвященной памяти А.А. Ляпунова (Новосибирск, 2001); на 4-м Международном студенческом научном конгрессе стран АТР "Fourth International Young Scholars' Forum of the Asia-Pacific Region Countries" (Владивосток, 2001); на 49-ой молодежной научно-технической конференции "Творчество молодых - интеграция науки и образования" (Владивосток, 2001); на 2-ом Всесибирском конгрессе женщин-математиков (Красноярск, 2002); 6-ой Международной конференции "Организация структур в открытых системах" (Алматы, 2002); на 6-ой, 7-ой и 8-ой Пущинской школе-конференции молодых ученых "Биология - наука XXI века" (Пущино, 2002, 2003, 2004); на 2-ой международной научной конференции "Рыбохозяйственные исследования Мирового океана" (Владивосток, 2002); на конференции "Вычислительные и информационные технологии в науке, технике и образовании" (Усть-Каменогорск, 2003) и на международной конференции "Physics and control. International conference" (Санкт-Петербург, 2003).
Публикации. Результаты диссертационной работы представлены в 34 публикациях.
Личный вклад автора. Автору принадлежит
математическая постановка задачи и выбор методов исследования. Кроме того, автором разработано
необходимое программное обеспечение, являющееся дополнительным инструментом для проводимого
в работе численного исследования; дана биологическая интерпретация полученных результатов.
В совместных работах автору принадлежит исследование линейного вида зависимости
приспособленности от численности.
Объем и структура диссертации. Диссертация состоит из введения, четырех глав и заключения, объем работы 185 страниц, содержит 81 иллюстраций, 4 таблицы. Список литературы включает 266 наименований, из них 126 на иностранных языках.
В главе 1 рассматриваются результаты математической популяционной генетики, касающиеся действия естественного отбора в менделевских популяциях с одним адаптивным локусом. Рассматриваются основные результаты антропогенного воздействия на численность и генетическое разнообразие.
В главе 2 исследовано действие плотностно-зависимого естественного отбора в менделевской однолокусной диаллельной популяции диплоидных организмов. Модель такой популяции представляет собой систему рекуррентных уравнений, связывающих частоты аллеля А (qn) и значения численности популяции (xn) в смежных поколениях:
|
|
(2.1) |
где 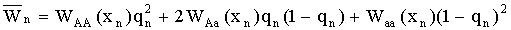 – средняя приспособленность
популяции в n-ом поколении, WAA, WAa,
Waa – приспособленность соответствующего генотипа, она равна отношению
половины числа гамет, продуцируемых данным генотипическим классом и вошедших в зиготы следующего поколения,
к численности этого генотипического класса (Fisher, 1930; В.А. Ратнер, 1973, 1977).
– средняя приспособленность
популяции в n-ом поколении, WAA, WAa,
Waa – приспособленность соответствующего генотипа, она равна отношению
половины числа гамет, продуцируемых данным генотипическим классом и вошедших в зиготы следующего поколения,
к численности этого генотипического класса (Fisher, 1930; В.А. Ратнер, 1973, 1977).
Перечислим основные предположения, принятые при построении модели (2.1). Рассматривается один диаллельный локус А с альтернативными вариантами гена А и а, причем фенотип особи жестко определяется ее генотипом. В популяции наблюдается панмиксия, выполняются менделевские правила наследования; считается, что половой процесс не связан с существованием дифференцированных полов. Из прямого рассмотрения исключена среда обитания организмов. Поколения считаются неперекрывающимися, т.е. родительское поколение, оставив потомство, элиминируется. Известны реальные популяции, обладающие этим свойством (например, однолетние растения, насекомые, мелкие грызуны, отдельные виды лососевых рыб).
В § 2.1 вводится следующий вид зависимости приспособленностей генотипов (Wij) от численности (x) популяции:
|
|
(2.2) |
где Rij и Kij – соответственно мальтузианский и ресурсный параметр ij-ого генотипа; i,j – принимают значения: А и а. Rij характеризует репродуктивный потенциал генотипа; а Kij – емкость экологической ниши: т.е. если вся популяция будет состоять только из особей с ij-м генотипом, ее численность составит величину Kij.
Интересна ситуация, когда существует численность x*, при
которой все генотипы имеют равные приспособленности:
Выделяются основные вопросы исследования диаллельной модели:
В § 2.2 найдены мономорфные стационарные точки
модели:
Утверждение 2.1. Точка пересечения графиков
приспособленностей всех генотипов x* соответствует численности полиморфной стационарной точки только в том случае,
когда все генотипы имеют одинаковые ресурсные параметры:
В этих случаях в стационарной точке частота аллеля A (q) может принимать любое значение. Если же существует разнообразие по ресурсным параметрам и мальтузианские параметры генотипов не тривиальны, то третья полиморфная стационарная точка имеет вид:
|
|
(2.3) |
Показано, что существование полиморфной стационарной точки зависит от взаимного расположения ресурсных параметров. Доказаны следующие утверждения:
Утверждение 2.2. Если гетерозигота обладает минимальным ресурсным
параметром
Утверждение 2.3. Если ресурсный параметр гетерозиготы
занимает промежуточное положение
Утверждение 2.4. Если гетерозигота имеет максимальный
ресурсный параметр
В § 2.3 получены условия устойчивости для мономорфных
стационарных точек: 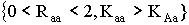 ; и
; и 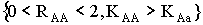 .
.
Утверждение 2.5. Если гетерозиготе соответствует минимальный
ресурсный параметр
Утверждение 2.6. Если ресурсный параметр гетерозиготы максимален
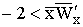 .
.
В § 2.4 проводится численное исследование динамического поведения модели в пространстве модельных параметров в соответствии с полученными условиями существования и устойчивости стационарных точек.
Проведенное исследование показывает, что мономорфизм или полиморфизм установится в популяции, во многом зависит от взаимного расположения ресурсных параметров генотипов и начальных условий. Выделены параметрические области различного динамического поведения модели в предположении, что изначально популяция полиморфна, так как очевидно, что в случае изначально генетически мономорфной популяции отбора нет, а динамика численности полностью определяется величиной мальтузианского параметра представленного генотипа:
KAa<KAA, KAa<Kaa. Мономорфизм. В зависимости от начального количественного преимущества и преимущества по ресурсному параметру закрепится аллель A или a. Численность популяции стационарна (x=K), если соответствующий мальтузианский параметр меньше двух; флуктуирует, если этот параметр больше двух.
Kaa<KAaа<KAA. Мономорфизм. Закрепляется аллель A. Если RAA<2, то численность стационарна (x=KAA); флуктуирует, если RAA>2. Если параметры гетерозиготы и гомозиготы AA близки, возможен полиморфизм, сопровождающийся колебаниями численности и генетического состава.
KAa>KAA,
KAa>Kaa. Полиморфизм.
Численность и генетический состав популяции стационарны, если 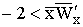 ;
иначе – флуктуируют.
;
иначе – флуктуируют.
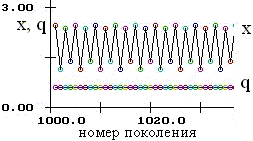 Рис. 2.1. Колебания численности (x) при постоянном генетическом разнообразии (частотах аллелей q). |
Проведенное исследование показывает, что на динамику популяции влияет не столько преимущество по мальтузианскому параметру отдельного генотипа, сколько преимущество по ресурсному параметру. Этот результат согласуется с аналогичными исследованиями Е.В. Евдокимова (1999) для гаплоидных организмов. Динамика численности и генетического состава популяции может быть стационарной либо флуктуирующей. Обнаружены устойчивые колебания численности при постоянном генетическом составе (рис. 2.1). |
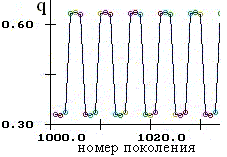
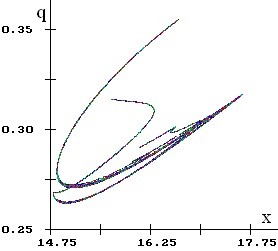
Возможны колебания численности и генетического состава одновременно, причем динамика может быть как регулярной (рис. 2.2), так и хаотической. В системе могут возникать странные аттракторы (рис. 2.3).

|
|
| Рис. 2.2. Регулярная динамика численности (x) и частоты аллеля А (q). Цикл длины шесть. | |
|
| Рис. 2.3. Фрагмент аттрактора дробной размерности D»1.339 |
§ 2.5 дополняет проведенное исследование рассмотрением
ситуации, когда в популяции нет разнообразия по ресурсным параметрам
Исследован случай, когда функции приспособленности вообще не пересекаются,
что достигается при выполнении следующего условия на параметры: 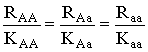 .
Интересно, что этом случае не было обнаружено колебаний генетического состава.
.
Интересно, что этом случае не было обнаружено колебаний генетического состава.
Для всех случаев в результате исследования аналитически найдены стационарные точки и условия их устойчивости. Проведено численное исследование динамики модели. Выделены параметрические области различного динамического поведения модели.
В главе 3 исследуется задача оптимального неселективного изъятия ("сбора урожая") из менделевской однолокусной популяции в равновесном режиме. Под оптимальным промыслом понимается промысел с "максимальным уравновешенным урожаем". Таким образом, при оптимальном промысле поддерживается такая доля изъятия из популяции, которая обеспечивает максимальный равновесный уровень промыслового "урожая" при достаточно долгом времени эксплуатации. Рассматриваются две возможные стратегии промысла: изъятие постоянной фиксированной части (доли) популяции и изъятие переменной доли, в зависимости от численности популяции.
§ 3.1 вводится промысел в модель динамики менделевской однолокусной диаллельной популяции диплоидных организмов при линейном лимитировании. Тогда система (2.1) с учетом ведения промысла принимает вид:
|
(3.1) |
где 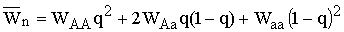 – средняя приспособленность,
– средняя приспособленность,
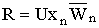 – промысел, U – доля изъятия.
– промысел, U – доля изъятия.
Утверждение 3.1. Снижение численности, вызванное промыслом, может перевести равновесное значение через x*, и в популяции кардинальным образом изменятся условия (точнее, тип) отбора.
Для доказательства данного утверждения необходимо рассмотреть отдельно, как влияет на динамику популяции каждая из возможных стратегий промысла.
В § 3.2 решается задача оптимизации
промысла при постоянной доле изъятия. Оптимальный равновесный уровень численности
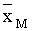 , обеспечивающий максимальный равновесный
уровень изъятия, однозначно определяется уравнением
, обеспечивающий максимальный равновесный
уровень изъятия, однозначно определяется уравнением 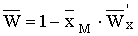
Оптимальная доля изъятия (в относительных
единицах численности) имеет вид 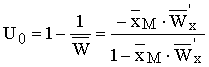
Найдены равновесные значения численности и частоты аллеля А модели (3.1), обеспечивающие максимальный объем изъятия.
Утверждение 3.2. В состоянии, обеспечивающем максимальный уровень изъятия, значение частоты аллеля А остается таким же, как и в случае, когда промысел отсутствует, а равновесное значение численности снижается в два раза.
Показано, что при линейном виде функций приспособленностей и при описанных соотношениях параметров модели значение стационарного генетического состава не зависит от стационарного значения численности.
Показано, что условия существования равновесных значений в целом при отсутствии промысла и при его воздействии одинаковы. Следовательно, полиморфное равновесное состояние не существует, когда ресурсный параметр гетерозиготы занимает промежуточное положение.
В § 3.3 получены условия устойчивости равновесных состояний.
Утверждение 3.3. Мономорфные равновесные состояния модели (3.1) устойчивы, если выполнено одно из следующих условий:
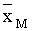
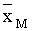 <x* и
<x* и 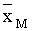 <x*,
<x*, При выполнении третьего условия в отсутствие промысла при таком расположении ресурсных параметров мономорфная стационарная точка неустойчива, а значение численности больше x*. Это означает, что снижение численности, вызванное промыслом, может перевести равновесное значение через x*, и в популяции кардинальным образом изменятся условия (точнее, тип) отбора. В результате, популяция из полиморфного состояния, которое наблюдалось в отсутствие промысла, перейдет в устойчивое мономорфное состояние. Таким образом, в этом случае промысел с постоянной долей изъятия приводит к разрушению полиморфизма и потере части разнообразия.
Утверждение 3.4.
При Rij, Kij>0
в полиморфном равновесном состоянии оптимальная доля изъятия больше нуля, а средняя
приспособленность больше 1, т.е. U0>0 и
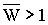
Утверждение 3.5. Полиморфное равновесное состояние модели (3.1) устойчиво, если выполнено одно из следующих условий:
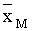 <x* и
<x* и 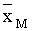 и
и 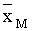 <x*,
<x*, При выполнении второго условия в результате промысла полиморфное состояние может стать устойчивым, в то время как в неэксплуатируемой популяции устойчивым является мономорфное состояние. Таким образом, промысел с постоянной долей изъятия может приводить к возникновению устойчивого полиморфизма в популяции.
В § 3.4 проводится численное исследование влияния промысла с постоянной долей изъятия на динамику популяции. Показано, что промысел при любой оптимальной доле изъятия ведет к стабилизации численности и частоты аллеля А. Кроме того, показано, что при оптимальном промысле с постоянной долей изъятия численность популяции сохраняется на равновесном уровне при любых значениях модельных параметров, но промысел может привести к изменению генетического разнообразия в случае, если какая-либо из оптимальных долей изъятия переведет равновесную численность через x*.
В § 3.5 решена задача оптимизации
промысла при переменной доле изъятия. В случае переменной доли изъятия функция объема
промысла 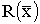 выбирается в виде "трофической"
функции с насыщением. В этом случае доля изъятия равна
выбирается в виде "трофической"
функции с насыщением. В этом случае доля изъятия равна
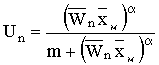 , где m – величина промысловых усилий,
обеспечивающая долю изъятия, равную половине от максимально возможной при заданном уровне
численности, a – параметр, характеризующий интенсивность
изменения промысловых усилий с ростом численности популяции.
, где m – величина промысловых усилий,
обеспечивающая долю изъятия, равную половине от максимально возможной при заданном уровне
численности, a – параметр, характеризующий интенсивность
изменения промысловых усилий с ростом численности популяции.
Показано, что оптимальная доля изъятия в относительных единицах численности не зависит от стратегии промысла, а определяется лишь величиной репродуктивного потенциала популяции. Также вычислено оптимальное значение промыслового параметра m.
В § 3.6 получены условия устойчивости равновесных состояний.
Утверждение 3.6. Если:
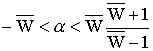 , то при выполнении условий утверждения 3.3.
в модели (3.1) устойчивы мономорфные равновесные состояния; при выполнении условий
утверждения 3.5. – устойчиво полиморфное состояние.
, то при выполнении условий утверждения 3.3.
в модели (3.1) устойчивы мономорфные равновесные состояния; при выполнении условий
утверждения 3.5. – устойчиво полиморфное состояние.
Для мономорфного состояния
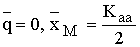 интервал устойчивости
интервал устойчивости
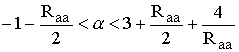 , для состояния
, для состояния
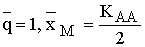 –
– 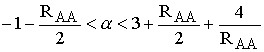 .
Таким образом, популяция может находиться в устойчивом равновесном
состоянии при таком же взаимном расположении ресурсных параметров,
как и в случае промысла с постоянной долей изъятия.
.
Таким образом, популяция может находиться в устойчивом равновесном
состоянии при таком же взаимном расположении ресурсных параметров,
как и в случае промысла с постоянной долей изъятия.
Показано, что промысел с переменной долей
изъятия может также привести к вымиранию популяции в случае, если начальное значение
численности 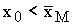 .
.
 |
 |
|
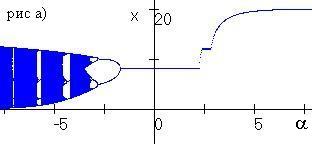
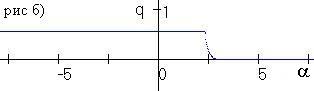
Рис. 3.1. Бифуркация численности (рис. а) и частоты аллеля A (рис. б) при изменении параметра a |
В § 3.7 проводится численное исследование влияния промысла с переменной долей изъятия на динамику популяции. Показано, что промысел с переменной долей изъятия может вызывать колебания численности, а также привести к изменению генетического разнообразия при переходе равновесной численности через x*. На рис. 3.1 приведена бифуркация численности и частоты аллеля А для системы (3.1), подверженной промыслу с переменной долей изъятия. Начальные параметры выбраны таким образом, что ресурсный параметр гетерозиготы минимален, в отсутствие промысла в популяции установится аллель а при стационарной численности. Как видно на рисунке, при a<–2 в модели устанавливаются полиморфизм при колебаниях численности. При –2<a<2 в популяции устанавливается полиморфизм при стационарной численности и оптимальном изъятии. При a>2.5 в популяции установиться аллель а при стационарной численности.
Глава 4 посвящена аналитическому и численному исследованию модели менделевской однолокусной популяции диплоидных организмов подверженной селективному промыслу с изъятием разных долей из каждого генотипического класса.
В § 4.1 описаны ограничения, принятые при построении модели и приведен вывод системы модельных уравнений (4.1).
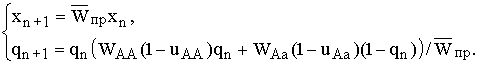 |
(4.1) |
где 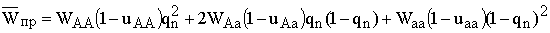 – коэффициент средней
приспособленности при изъятии разных долей из каждого генотипического класса.
– коэффициент средней
приспособленности при изъятии разных долей из каждого генотипического класса.
В § 4.2 в рамках аналитического исследования системы (4.1) показано, что параметрам данной модели можно поставить в соответствие параметры модели в отсутствие промысла. Показано, что при введении новых функции приспособленностей x* не является точкой пересечения графиков функций. Значит, данную модель нельзя свести к рассмотренным ранее, т.к. в предыдущих случаях весьма существенную роль оказывало расположение ресурсных параметров модели относительно x*. Если отказаться от оптимальности промысла, то в этом случае трудно определить, как численно изменится значение стационарной численности относительно той, которая была в отсутствие промысла даже для мономорфных равновесий.
В § 4.3 исследуется динамическое
поведение модели. Рассматриваются случаи различного положения ресурсного параметра
гетерозиготы. В случае, когда ресурсный параметр геторозиготы максимален, показано,
что если доля изъятия из гомозиготного генотипического класса больше, чем изъятие
из гетерозиготного класса, то при изменении доли изъятия из другого гомозиготного
класса в популяции возможны совместные колебания численности и генетического состава.
При
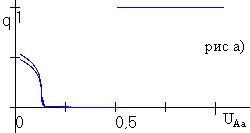
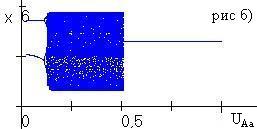 Рис. 4.1. Бифуркация частоты аллеля А (рис. а) и численности (рис. б) при изменении доли изъятия uAa при фиксированных uAA=0.5, uaa=0. |
В случае, когда ресурсный параметр гетерозиготы занимает промежуточное значение, в популяции в отсутствие промысла возможен полиморфизм, не связанный с существованием полиморфного равновесия. Проведенное численное исследование при промысле показало, что если доля изъятия из гомозиготных классов больше доли изъятия из гетерозиготного генотипического класса, то в популяции устанавливается полиморфизм либо наблюдаются колебания генетической структуры (рис. 4.1). Мономорфизм в популяции возможен только в тех случаях, когда доля изъятия из гетерозиготного класса больше доли изъятия любого из гомозиготных классов. Численное исследование в случае, когда ресурсный параметр гетерозиготы минимален, показало, что если доля изъятия из гетерозиготной группы меньше доли изъятия из гомозиготной группы, то в популяции возможно установление полиморфизма. В противном случае в популяции возможна смена устойчивости гомозиготных состояний. |
Показано, что отбор способствует закреплению генотипа с максимальным ресурсным параметром; значения мальтузианских параметров определяют характер динамики популяции.
Показано, что положение численности популяции в полиморфных стационарных точках относительно численности в мономорфных (как и их устойчивость) определяется соотношением значений ресурсных параметров гетерозиготы и гомозигот.
Решена задача оптимизации промысла для двух стратегий промысла. Показано, что оптимальная доля изъятия не зависит от рассматриваемых стратегии промысла.
Показано, что оптимальный промысел с постоянной долей изъятия стабилизирует популяционную динамику. Промысел с переменной долей изъятия может вызвать колебания численности, а при определенных начальных условиях – даже привести к вымиранию популяции.
Показано, что промысел может привести к изменениям результатов отбора и вызвать разрушение или способствовать поддержанию полиморфизма.
Построена математическая модель, учитывающая воздействие селективного промысла при разных долях изъятия из каждого генотипического класса. Показано, что если в отсутствие промысла в популяции преобладает один из генотипов, то при изъятии бόльшей доли из этого класса в популяции возможна смена устойчивости гомозиготных состояний. Если изымать из других классов, то можно сохранить генетическое разнообразие в популяции.
Колчинская О.Л., Павлова (Колбина) Е.А. Исследование в модели плотностно зависимого отбора в менделевской лимитированной популяции // Труды ДВГТУ. Вып. 124. Владивосток: ДВГТУ, 1999. С. 55-60.
Колчинская О.Л., Павлова (Колбина) Е.А. Проблемы регулярного поведения и детерминированного хаоса в менделевской лимитированной популяции // Труды ДВГТУ. Вып. 127. Владивосток: ДВГТУ, 2000. С. 44-47.
Жданова О.Л., Павлова (Колбина) Е.А., Фрисман Е.Я. Проблемы регулярного поведения и детерминированного хаоса в менделевской лимитированной популяции // 6 межд. конф. "Экология и здоровье человека. Экологическое образование. Математические модели и информационные технологии". Краснодар, 2001. С. 70.
Фрисман Е.Я., Павлова (Колбина) Е.А., Жданова О.Л. Колебания генетической структуры и численности в математических моделях эволюции менделевских лимитированных популяций // Сборник докладов конф., посв. 90-летию А. А. Ляпунова. Новосибирск, 2001. С. 692-699.
Павлова (Колбина) Е.А., Фрисман Е.Я. Изучение сценариев перехода к хаотической динамике численности менделевской лимитированной популяции в естественных условиях и при антропогенном воздействии // Моделирование неравновесных систем - 2001: Материалы IV Всероссийского семинара. Красноярск: ИПЦ КГТУ, 2001. С. 110-111.
Pavlova (Kolbina) E.A., Zhdanova O.L. Problems of regular behaviour and determined chaos in mendel limited population // 4-th Intern. Young Sch. Forum of the Asia-Pacific Reg. Countries. Proceeding. Part I. Vladivostok: FESTU publ. house, 2001. P. 121.
Павлова (Колбина) Е.А. Колебания генетической структуры и численности в математической модели динамики менделевской лимитированной популяции в естественных условиях и при воздействии промысла // Сборник докладов 49-й молодежной научно-технической конференции "Творчество молодых – интеграция науки и образования". Владивосток: Мор.гос.ун-т, 2001. С. 117-120.
Павлова (Колбина) Е.А. Изучение сценариев перехода к хаотической динамике менделевской популяции в естественных условиях и при воздействии промысла // Рыбохозяйственные исследования Мирового океана: Труды II Межд. конф.: в 2 т. Т. 2. Влад-к: Дальрыбвтуз, 2002. С. 56-57.
Колбина Е.А. Аналитическое исследование частного случая в модели эволюции менделевской популяции диплоидных организмов // МНС – 2002: Материалы V Всероссийского семинара. Красноярск, 2002. С. 98-99.
Колбина Е.А. Проблемы регулярного поведения и детерминированного хаоса в математической модели менделевской линейно лимитированной популяции в естественных условиях и при воздействии промысла // Тезисы докладов 6-ой международной конференции "Организация структур в открытых системах – 2002". Алматы, 2002. С. 59-60.
Колбина Е.А. Об одном частном случае в модели эволюции менделевской лимитированной популяции диплоидных организмов // Труды ДВГТУ. Вып. 132. Владивосток: ДВГТУ, 2002. С. 201-203.
Колбина Е.А. Проблемы регулярного поведения и детерминированного хаоса в математической модели менделевской линейно лимитированной популяции в естественных условиях и при воздействии промысла // Проблемы эволюции открытых систем. Вып. 5. Т. 1. Алматы, 2003. С. 210-214.
Колбина Е.А. Изучение сценариев перехода к хаотической динамике менделевской популяции // 7-ая Пущинская школа-конференция молодых ученых. Сборник тезисов. Пущино, 2003. С. 250-251.
Frisman E.Ya., Kolbina E.A., Zhdanova O.L. Problems Of Regular Behaviour And Determined Chaos In Mathematical Modeles Of Mendelian Limited Populations // Intern. Conf. "Physics and Control". Saint Petersburg, 2003. P. 666-669.
Жданова О.Л., Колбина Е.А., Фрисман Е.Я. Проблемы регулярного поведения и детерминированного хаоса в математической модели эволюции менделевской лимитированной популяции // Дальневосточный математический журнал. Т. 4. № 2. Владивосток, 2003. C. 289-303.
Колбина Е.А. Изучение динамических последствий оптимального управления в менделевской популяции// ХХХ дальневосточная мат.школа-семинар им. Е.В.Золотова: тез. докл. Хабаровск, 2005. С. 84.